Optimal Gait Control for a Tendon-driven Soft Quadruped Robot by Model-based Reinforcement Learning (ICRA 2025)

Post's content provided by: Xuezhi

Authors: Xuezhi Niu*, Kaige Tan*, Didem Gürdür Broo and Lei Feng
Soft quadrupeds are lightweight and safe around people, but their deformable bodies make gait control hard. We use model-based reinforcement learning (MBRL) with a learned surrogate model plus post-training (PT) in high-fidelity Simscape to get fast, stable gaits for SoftQ, a tendon-driven quadruped with four compressible soft actuators. Compared with model-free RL and an expert trot controller, our policy is faster, more stable, and more energy-efficient.

Highlights:

Surrogate-guided SAC converges quicklyon the proxy model, then PT refines the policy on Simscape.
Reduced action/state spaces via gait parametrization and IK improve training efficiency and safety.

Introduction

Our previous studies (Ji et al., 2022, Ji et al., 2022) develop SoftQ (Soft Quadruped), a soft quadruped robot enabled by four Compressible Tendon-driven Soft Actuators (CTSAs) as legs. However, two limitations are observed during the learning-based gait design. First, the underlying simulation model of the SoftQ by SimScape is accurate but time-consuming, necessitating around 30 seconds of computation for each elapsed physical second. Second, we performed an end-to-end control by directly using the motor output as the action space. Despite the simplicity, it is inefficient for mobile robots due to the generation of numerous unfeasible or redundant leg motor position combinations, by which the learning process does not exploit the model knowledge of the SoftQ.

Why soft quadrupeds?

Affordability: 3D-printable CTSAs simplify fabrication and maintenance
Efficiency: Reduced mass lowers energy consumption during locomotion
Safety: Soft robots are lightweight and safe to interact with, ideal for dynamic environments

”Model” Explained

The SoftQ is characterized by its innovative utilization of four CTSAs. Provides an illustration of the robot, including orientation (roll $\theta_x$, pitch $\theta_y$, and yaw $\theta_z$), translational velocities along three axes ($v_x, v_y, v_z$), and contact forces on its four feet ($f_\textrm{nFL}, f_\textrm{nFR}, f_\textrm{nRL}, f_\textrm{nRR}$, FL = front left, RR = rear right). The defining characteristic of the CTSAs is the cable-driven mechanism, which can continuously bend and twist. The cables, also referred to as tendons, guide the deformation of soft materials. Each leg of the robot is actuated by three cables, controlled by three servo motors, resulting in a total of 12 actuators for the robot's overall motion. Thus, the direct control input to each leg is a vector $\mathbf{d}_\textrm{ten} = \left[d_\textrm{A}, d_\textrm{B}, d_\textrm{C}\right]^\top$. As illustrated in , the tendon force is applied to the actuator and activates its deformation, and $\mathbf{d}_\textrm{ten}$ controls the deformation degree on each leg.

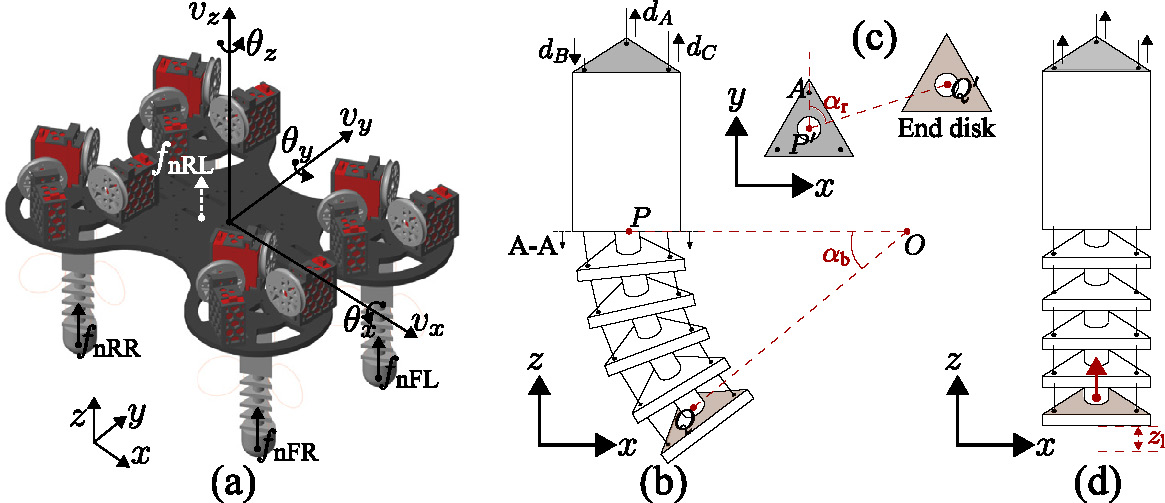
Overview of SoftQ and CTSA: (a) Rendered robot with key states. (b) CTSA bending angle $\alpha_b$. (c) CTSA rotational angle $\alpha_r$. (d) CTSA compression length $z_\textrm{l}$.

Based on the control input definition, a leg's pose during the walking can be characterized by three values illustrated in. $\alpha_\textrm{b}$ is the bending angle of a leg, $\alpha_\textrm{r}$ is the rotational angle of a leg, and $z_\textrm{l}$ is the compression length of a leg. A combination of the three values defines the pose of the leg $\mathbf{a} = [\alpha_\textrm{b}, \alpha_\textrm{r}, z_\textrm{l}]^\top$. The pose and the movements of the three servo motors satisfy the inverse kinematic model with $$\mathbf{d}_\textrm{ten} = g_\textrm{inv}(\mathbf{a}) = f_\textrm{inv}([\alpha_\textrm{b}, \alpha_\textrm{r}]^\top) + \textbf{1} z_\textrm{l},$$ where $f_\textrm{inv}: \mathbb{R}^2 \rightarrow \mathbb{R}^3$ is derived through geometric analysis, and $$d_\textrm{A} = R_\textrm{d} \alpha_\textrm{b} \cos(\alpha_\textrm{r})+z_l,\\ d_\textrm{B} = R_\textrm{d} \alpha_\textrm{b} \cos(\alpha_\textrm{r}+\frac{2\pi}{3})+z_l,\\ d_\textrm{C} = R_\textrm{d} \alpha_\textrm{b} \cos(\alpha_\textrm{r}+\frac{4\pi}{3})+z_l.$$ The vector of tendon displacement $\mathbf{d}_\textrm{ten}$ is further used as the motor reference for the low-level position control. The synchronization of the designed trajectory on $\mathbf{a}$ and $\mathbf{d}_\textrm{ten}$ of each leg will lead to a gait pattern of the robot.

Model-based Reinforcement Learning

Surrogate model: DNN $\hat{f}_\theta (\mathbf{s},\mathbf{a})$ trained on ~250 randomized rollouts from Simscape, predicting next state from current state and action. New interactive actions $[\alpha_{\textrm{b}_\textrm{1}}, z_{\textrm{l}_\textrm{1}},\alpha_{\textrm{b}_\textrm{2}}, z_{\textrm{l}_\textrm{2}}]$ from domain knowledge.
Policy/algorithm: Reuse the surrogate to train SAC policy; Post Training reuses the converged SAC policy and fine-tunes on Simscape with adjusted learning rates and reward coefficients.
Reward: Track forward speed, stay upright, discourage jerky and over-bent legs; includes action-acceleration and posture penalties.

How the model is built

Surrogate Fitting: Train a Deep Neural Network (DNN) $\hat f_\theta$ to approximate the robot dynamics.
RL with Surrogate: Train RL policy with the surrogate model using Soft Actor-Critic (SAC).
Post Train: Refine the learned policy in the full SimScape model to close the reality gap.

Results at a Glance

Training speed: MBRL+PT converges in ~60 episodes on Simscape; model-free RL needs ~450 episodes. Time efficient 10.5 h (avg) vs 22.6 h (MFRL).
Energy efficiency: Cost of Transport ≈68 J/kg/m (avg) vs 501 J/kg/m for model-free; expert trot ≈ 81 J/kg/m.
Stability score: 0.65 (avg) vs 0.03 for model-free.
Speed (simulation): Up to 0.36 m/s; average 0.26 m/s across settings.
Speed (real robot): ~0.15 m/s on SoftQ with onboard sensing, improving prior model-free baseline (~0.05 m/s).

From simulation to hardware

We deploy the controller on SoftQ using a Raspberry Pi + STM32 stack, 50 ms control step, IMU and ToF sensors, and PD motor loops. A simple expert trot is used for short warm-starts during PT; Kalman filtering and contact binarization help with noise. The robot walks 1.5 m and stops at 0.1 m from a wall, matching the learned behavior.

Citation

If you find the idea useful, please consider citing our work:

                                            
                                            
                                                @inproceedings{niu2025optimal,
                                                author = {Niu, Xuezhi and Kaige, Tan and Broo, Didem Gürdür and Lei, Feng},
                                                publisher = {IEEE},
                                                series = {2025 IEEE International Conference on Robotics and Automation (ICRA)},
                                                title = {{Optimal Gait Control for a Tendon-driven Soft Quadruped Robot by Model-based Reinforcement Learning}},
                                                year = {2025}
                                                }